Intent
We follow a spiralling curriculum that aims to develop our students’ mathematical knowledge to permit them to become independent able problem solvers who are not afraid to take risks.
We aim to create an inclusive and reflective learning environment that stimulates lifelong mathematicians who become fluent in the fundamentals of mathematics, developing the confidence to apply their mathematical skills and abilities.
Students must be able to accurately recall and apply facts that allow them to master skills and reason mathematically. Given full access to a high-quality mathematics curriculum which is both challenging and enjoyable, allowing for connections in their learning to be made providing a greater depth of understanding.
The intention of our curriculum is to allow students to:
- become fluent in the fundamentals of mathematics
- reason mathematically
- problem-solve by applying their mathematics
At St Michael’s we are committed to ensuring that children are able to recognise the importance of mathematics in the wider world. We want students to gain cultural capital to embed the knowledge they need to prepare them for their future accomplishments. Our discovery curriculum for Year 7 builds on the Cultural Capital of our students where students learn about the history of codes and encryption from ancient civilisations up to the present day. Our discovery curriculum introduces students to the stories of some of the most influential mathematicians throughout history and the impact that their work has had on the world we live in.
We want all children to enjoy mathematics and to experience success in the subject, with the ability to reason mathematically. We are committed to developing children’s curiosity about the subject, as well as an appreciation of the beauty and power of mathematics.
The further rationale behind our curriculum design includes trying to make learning become retained in the working memory by having a spiral curriculum. The six main areas of number, algebra, ratio, proportion and rates of change, geometry and measures, probability and statistics are taught in a cycle. Each time students revisit an area, they are exposed to more complex content, building on what they have previously learnt. We ensure the level of challenge is high enough for the most able, with scaffold and support available for students who need it.
Implementation
The mathematics department at St Michael’s operates using a spiral curriculum design that is a cognitive theory proposed by Jerome Bruner, based on the iterative revisiting of topics at increasing levels of difficulty. New skills and notions are clearly related to previous learning, to progressively increase competency (Johnston, 2012; Harden, 1999). Spiral curricula fit well with enquiry-type learning subjects (Wilson et al., 2015) which is why we designed this curriculum methodology. This curriculum model allows staff to focus on embedding challenge, metacognition, memory techniques and literacy into lessons.
Nevertheless, it would be wrong to say that altering our curriculum has had no effect on our pedagogy. Instead of a linear progression, we now see the GCSE course as a web of linked ideas.
A visual demonstration of how a spiralling curriculum may be utilised is below:
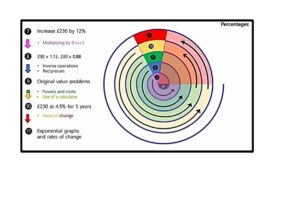
At St Michael’s we also adopt diagonal sequencing tracking so that we are aware when students study cross-curricular topics in other subjects.
We utilise a variety of techniques to emphasise this in our teaching.
- Practise and consolidation play a central role. Carefully designed variation within this builds fluency and understanding of underlying mathematical concepts.
- Our questioning requires students to make connections between topics, which teaches them the important study skill of elaboration (Dunlosky, 2013).
- New learning is promoted through demonstration, collaborative learning and purposeful-practice.
- Recall of knowledge is promoted by regular low-stakes quizzes.
- Students have access to one-page summaries of each unit they have studied.
- Our Knowledge organisers provide a heavy focus on tier-three vocabulary to improve students cognitive understanding and allow the working memory to focus on mathematical processes required in their learning.
- A mixture of assessment strategies is utilised throughout the curriculum that underpins formative and summative techniques.
- Feedback is given to students where they have the ability to reflect and develop an understanding of topics they previously felt difficult. We utilise formal assessments to generate a consistent approach to the development of our students.
- Feedback to half-termly assessments is now given through the ipsative method which Wallace (2015) describes as ‘ipsative assessments are a type of assessment in which the learner’s current level of achievement, skill, knowledge or understanding is assessed against their own previous level, rather than against fixed criteria or a norm.’ Therefore, students are provided with an ipsative grade such as “+15 marks” or “Ipsative grade: +0.5” rather than the more common “you achieved a grade 5.”
By splitting large topics into smaller sections, students can be exposed to multi-topic exam-style questions early in their studies and encouraged to view mathematics as the complex, holistic subject that it is.
Impact
Since the GCSE curriculum was updated with 9-1 replacing A*-G grades, we have ensured that that curriculum content offered at St Michael’s matches the rigour and development of a broad depth of mathematical skills and knowledge. We know our curriculum is working in the Mathematics department through the steep improvement of the department’s GCSE results and contextual GCSE results. The impact of our mathematics curriculum is that children understand the relevance of what they are learning in relation to real-world concepts. We have fostered an environment where mathematics it is acceptable to be ‘wrong’ because the journey to finding an answer is most important. Our children have a growth mindset and they make measurable progression against their own targets.
KS3 students are now provided with opportunities to access GCSE content immediately, which offers challenge and ensures there are no wasted years. Our KS4 students are provided with an in-depth curriculum which develops their ability to apply problem-solving strategies to content.
Students that require additional support in mathematics can follow a bespoke curriculum, which is tailored for their academic needs. Students follow individual flight paths for their end of year targets and pupil progress is tracked through regular marking and feedback in addition to formal assessments each year.
Throughout our curriculum, we also aim to ensure our pupils gain a love and appreciation for all the mathematics around them and will fully enjoy mathematics. The three key principles of our curriculum are:
Deep Understanding
Our practice embeds the importance of deep understanding, as equating progress with learning new procedures and rules means many students will miss out on a depth of understanding. We achieve this by allowing the pupils to represent concepts in a variety of different ways.
Mathematical thinking
We believe that it is essential for students to develop mathematical thinking in and out of the classroom to fully master mathematical concepts. We want students to think like mathematicians, not just DO the mathematics. We believe that during the learning experience students should; explore, wonder, question, conjecture, experiment and make theories in order to guide their own journey.
Mathematical Language
We believe that pupils should be encouraged to use mathematical language throughout their mathematics learning to deepen their understanding of concepts.
The way students speak and write about mathematics has been shown to have an impact on their success in mathematics. We, therefore, use a carefully sequenced, structured approach to introducing and reinforcing mathematical vocabulary throughout mathematics lessons, so students have the opportunity to work with word problems from the beginning of their learning. Our Knowledge organisers also provide a heavy focus on tier three vocabulary to improve their cognitive understanding and allow the working memory to focus on mathematical processes required in their learning.
Alongside these three key principles problem solving is at the heart of mathematics. Our aim is to create the optimal conditions for students to learn through problem-solving and to learn to develop lifelong transferable skills.
Constant reflection and feedback ensure that improvements are made to the curriculum each year.
Students also get opportunities to engage with:
- STEM
- UK Mathematics Challenge
- PiXL
- Nrich
- A-level content
- Tutoring opportunities
- Aim Higher initiatives